Distances in Machine Learning (Pt.1 – Traditional Distances)

While you were reading about machine learning or developing your own algorithms, you may have come across the term distance. This is natural, since we often want to know how far apart two things are: instances that are very close together in our representational space are probably in the same class; model predictions that are very far away from the ground truth indicate that our model should update itself significantly.

We can understand the gist of the concept from the its plain-language meaning: a distance function really does tell us how far apart two objects are. But did you know that distance functions are precisely defined mathematically?

This comes in handy, since it turns out there are so many types of objects that we might want to separate. No matter what type of objects we are measuring distances between, though, mathematicians have established that there are four characteristics shared by all functions that are suitable to use as distance functions:

1. Non-negativity. Distances can never be less than 0, which matches our common sense understanding that a distance is a magnitude.
2. Symmetry. The distance between any two objects \(A\) and \(B\) is the same as the distance between \(B\) and \(A\).
3. Identity of indiscernibles. The distance between an object \(A\) and itself is always 0.
4. Triangle inequality. The distance between two objects \(A\) and \(C\) is always less than or equal to the distance of traveling from \(A\) to \(B\) and then to \(C\).

Starting from these properties, we can then see that there are a number of machine learning scenarios where we would want to use distance functions.

We start with a distance function that aligns perfectly with our plain-language understanding of what a distance is. The Euclidean distance is the mathematical equivalent of the kind of distances we think about in everyday life.

On a map, we can think of the Euclidean distance as being how far apart two points are “as the crow flies.” In two-dimensions we calculate the distance between two points \(A = (A_x,A_y)\) and \(B = (B_x,B_y)\) as $$d(A,B) = \sqrt{(A_x – B_x)^2 + (A_y – B_y)^2}.$$

The Euclidean distance is related to the Pythagorean Theorem, which tells us that the distance squared between two points (the hypotenuse) is equal to the sum of distances squared between those two points in each dimension. In three-dimensional space we can use the Euclidean distance to express how far a robotic arm is from its goal, and the notion generalizes to higher dimensions as well.

Another kind of distance that we understand intuitively is the Manhattan–or City Block–distance. Instead of measuring distance as a straight line between two points, the Manhattan distance measures how long it is from \(A\) to \(B\) if we are restricted to moving in discrete amounts along any axis. This is typically visualized as having to walk along the regular blocks of a large city.

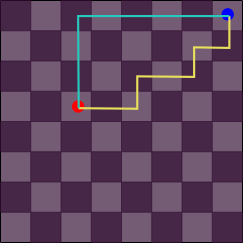
The Manhattan distance makes sense if we are restricted to moving in one dimension at a time. If we have a robotic arm that moves uniquely in the x, y, and z dimensions then we may be interested to know how long a path it will have to trace to move from \(A\) to \(B\). Mathematically, this is $$d(A,B) = |A_x – B_x| + |A_y – B_y| + |A_z – B_z|.$$

Yet another way of considering distance in our traditional sense is the Chebyshev distance, where the distance between two points is the greatest in any single dimension. This concept occurs naturally in scenarios where distances in some dimensions are subsumed by the effort of closing the distance in other dimensions. The classic example of this is measuring how far two squares on the chessboard are based on how many moves it would take a King to move between them.

Consider our example of the robotic arm, where each individual movement is restricted to a particular range. Maybe this is to guarantee that our robot can properly use sensor feedback to plan its follow-on movements. Then the Chebyshev distance tells us how many commands must be issued to move from \(A\) to \(B\). Mathematically, this is expressed as $$d(A,B) = \max_i |A_i – B_i|.$$

These three distances are just a brief sample of the kinds of traditional distances that we see in machine learning. They are used whenever we want to determine how far apart two instances are within our representational space. Some examples of this include

1. The k-means clustering algorithm assigns points to \(k\) clusters in such a way as to minimize the squared Euclidean distance between points and their respective cluster centres.
2. The k-nearest-neighbours classification algorithm labels an instance based on the labels of the \(k\) closest instances from memory.
3. For soft-margin support vector machines, misclassified instances can be tolerated as long as they are “close enough” to the separating hyperplane.

An important consideration for any of these distances is that we want to normalize our data before calculating distances. The purpose of normalization here is to ensure that each dimension has the same scale as the others. This avoids the scenario where distances in one dimension overwhelm all the other dimensions, preventing them from helping to separate instances.

Not every scenario where we want to measure distances will lend itself naturally to the types of distances we have covered in this post.

In Part 2, we will talk about different ways to measure the distance between two strings of characters.