Distances are used throughout machine learning to help us (and our algorithms) figure out many things such as how far apart two instances are or how far our prediction is from the ground truth. The first part of this series looked at traditional distances that line up with our every day experience with the word, but the mathematical possibilities are so much broader than this.
Consider individual words, or strings to computer scientists. We have an idea that the string pair is closer to the string part than it is to the string clod, but how can we formalize this?
If we wanted to use our traditional distances we would have to find a way to embed these strings in a representational space and then measure distances between the points representing the pair/part and pair/clod strings. This seems awkward and there is a better way: we can use string distances.
Hamming Distance
A simple way to measure this distance for strings of the same length is to count the number of characters that differ. This is the number of substitutions that are necessary to turn one string into the other.

The Hamming distance is useful for determining how many errors may have occurred in transmitting our string, which is useful for error-detecting and error-correcting codes. Consider a situation where we know that at most two characters can be substituted. If we use a code where all the strings are separated by a Hamming distance of 3 or greater, then we will always be able to detect the errors that occur. Alternatively, if we know that at most one character can be substituted then these codes can detect and correct the errors that occur, since only one code string will be a Hamming distance of 1 away from the string we receive.
Levenshtein Distance
The Hamming distance is quite straight-forward, but it is also restricted to the case where our two strings have the same distance. The real-world isn’t always so neat and simple, however. Happily we can extend the Hamming distance to the Levenshtein distance with some additional string operations: now we consider insertions, deletions, and substitutions.

The Levenshtein distance lets us consider string correction problems more generally and is related to problems of finding the longest common subsequence between two strings and DNA sequence alignment in bioinformatics.
Dynamic Time Warping
What if the strings we wanted to measure distances between weren’t strings at all, but were instead more generic sequences? In this case we can use a technique called dynamic time warping, which finds the optimal way of warping two temporal sequences into alignment. This allows us to calculate, for example, how similar two gaits are, even if the people are walking at different speeds.
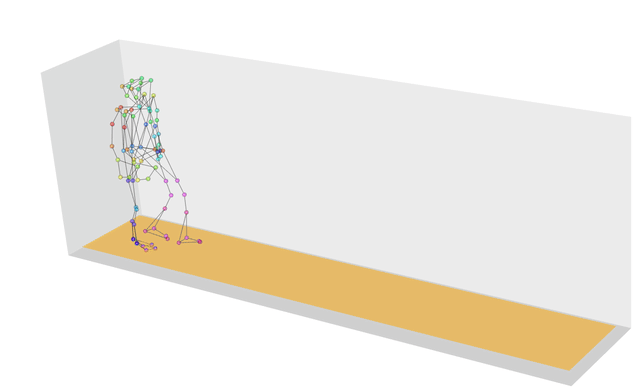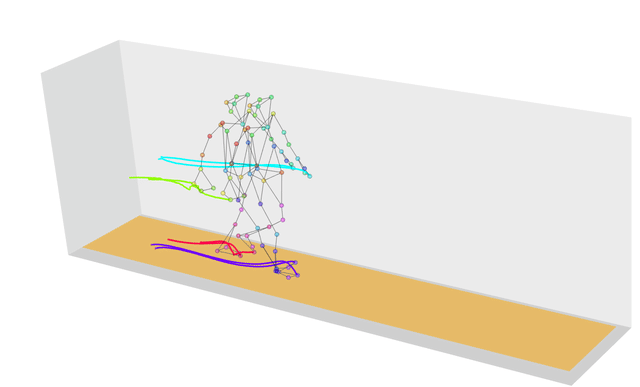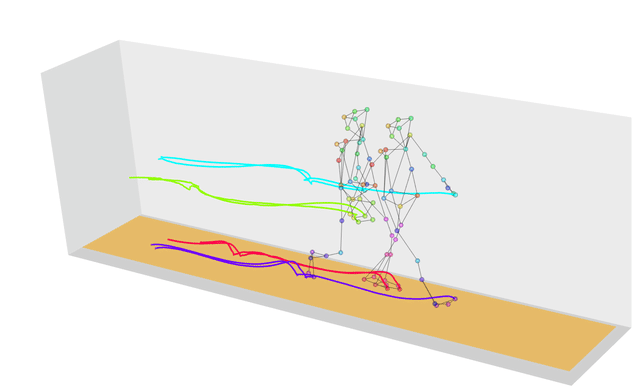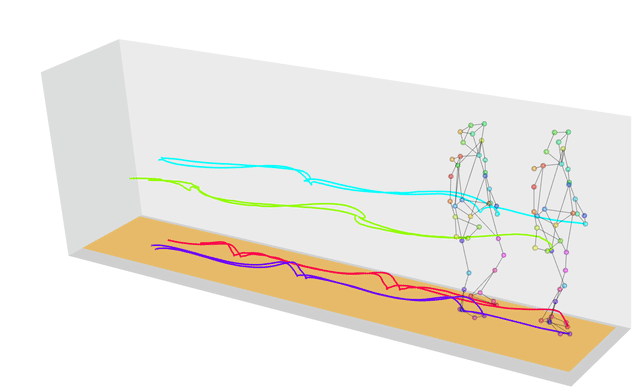
If you’re wondering why we have a similarity function in this list, that’s because similarity is just the inverse of distance! The more similar two objects are the closer they will be; the further apart two objects are the more different they will be.
Distances in Machine Learning
These distances and similarity functions are just some of the ways we can measure how similar two sequences are: whether these are sequences of characters, numbers, or anything else we like. We see string distances in machine learning, data mining and data analysis throughout our modern world:
- by the spell checker in your word processor to suggest correct words;
- in bioinformatics to judge how close two DNA sequences are to one another; and
- by our smart phones and computers to automatically correct transmission errors.
More Kinds of Distances
There are even more types of distances in machine learning and data mining than we’ve covered in these first two parts.
Check out Part 3 to learn how we can measure the distance between two models.

